In this part we’ll cover and properly define a very misunderstood concept in physics, power and energy.
Let’s start with defining power properly.
Power
Power can be defined as:
Rate of energy transferred, or work done, per unit of time.
In electrial circuits, we can define power, $P$, as: $$ P = V \cdot\ I $$
We measure power in watts, which we can define as: $$ 1\ W = \frac{1\ J}{s} = \frac{1\ N \cdot\ m}{s} = 1 kg \cdot\ m^{2} \cdot\ s^{-3} $$
We’ll mainly only encounter the $P = V \cdot\ I$ variant, however.
Using Ohm’s law that we learned from Part 1 we find that: $$ P = V \cdot\ I = \frac{V^2}{R} = I^2\ R $$
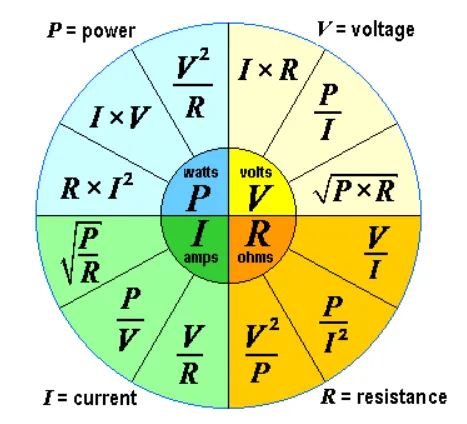
We can throw around this equation as much as we want and need, here’s a picture that illustrates all the possible combinations:
Energy
Energy can be defined as:
The capacity to do work in a given time.
Or in math terms: $$ W = \int_{t_1}^{t_2} P(t) dt $$
So, therefore:
- Power is Energy per unit of time.
- Energy is Power over time.
Positive and negative power
One small note here is that, power can end up being negative, which can be confusing at first.
We view this as we’re supplying power into a system. Therefore, positive power is consuming the power.
So:
- Positive: Power being consumed
- Negative: Power being supplied
Equivalent resistance
As we saw in the first part, we covered that in series circuits, the current needs to be the same. While in a parallel circuit, the voltage will need to be the same. We can use this to our advantage and find how we can simplify our circuits when we have a lot of resistors.
Equivalent resistance in series circuits
If we have a simple circuit of three resistors like this:
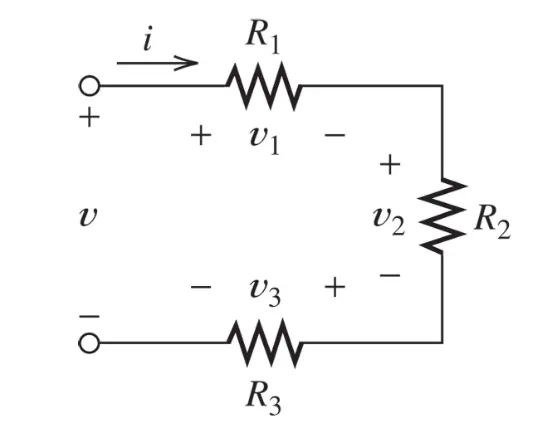
Using Ohm’s law and the fact that we know this is a series circuit we can find: $$ V = v_1 + v_2 + v_3 \newline V = I \cdot\ R_1 + I \cdot\ R_2 + I \cdot\ R_3 \newline V = (R_1 + R_2 + R_3) \cdot\ I \newline V = R_{eq} \cdot\ I $$
Where $R_{eq}$ is: $$ R_{eq} = R_1 + R_2 + R_3 $$
Or, more generally, if we have $N$ resistors in series, we can find the equivalent resistors as: $$ R_{eq} = R_1 + R_2 + \ldots\ + R_N $$
Equivalent resistance in parallel circuits
Now, if we instead have three parallel resistors instead like:
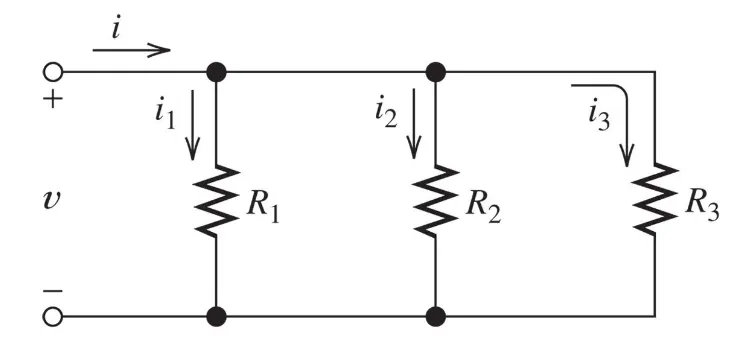
Again, using Ohm’s law and the fact that this is a parallel circuit we can find: $$ I = I_1 + I_2 + I_3 \newline I = \frac{V}{R_1} + \frac{V}{R_3} + \frac{V}{R_3} \newline I = (\frac{1}{R_1} + \frac{1}{R_3} + \frac{1}{R_3}) \cdot\ V \newline $$
Which means our $R_{eq}$ is: $$ \frac{1}{(\frac{1}{R_1} + \frac{1}{R_3} + \frac{1}{R_3})} $$
Another way of writing this is: $$ \frac{R_1\ R_2\ R_3}{R_1\ R_2 + R_2\ R_3 + R_1\ R_3} $$
Current and Voltage dividers
If we have this circuit:
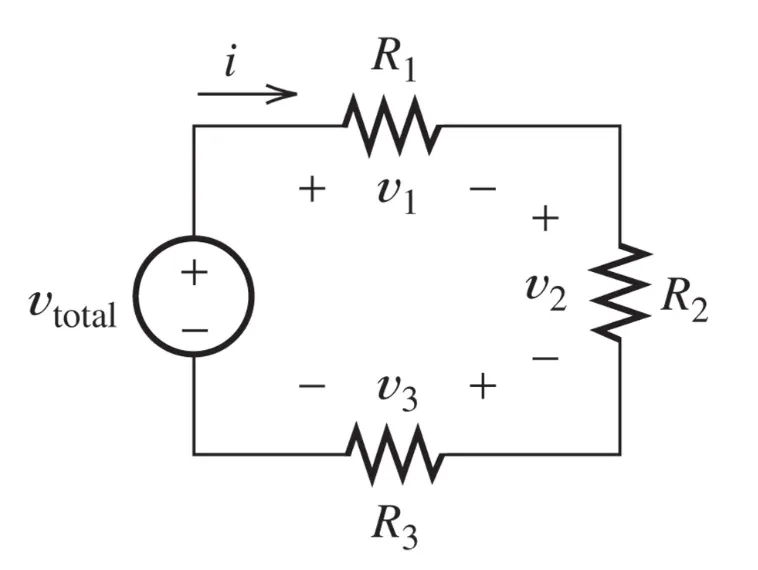 $$
R_{eq} = R_1 + R_2 + R_3 \newline
I = \frac{V_{total}}{R_{eq}}
$$
$$
R_{eq} = R_1 + R_2 + R_3 \newline
I = \frac{V_{total}}{R_{eq}}
$$
We can find equations for the relative voltages: $$ V_1 = I \cdot\ R_1 = V_{total} \cdot\ \frac{R_1}{(R_1 + R_2 + R_3)} \newline V_2 = I \cdot\ R_2 = V_{total} \cdot\ \frac{R_2}{(R_1 + R_2 + R_3)} \newline V_3 = I \cdot\ R_3 = V_{total} \cdot\ \frac{R_3}{(R_1 + R_2 + R_3)} \newline $$
This is what we call a voltage divider.
If we instead have this circuit:
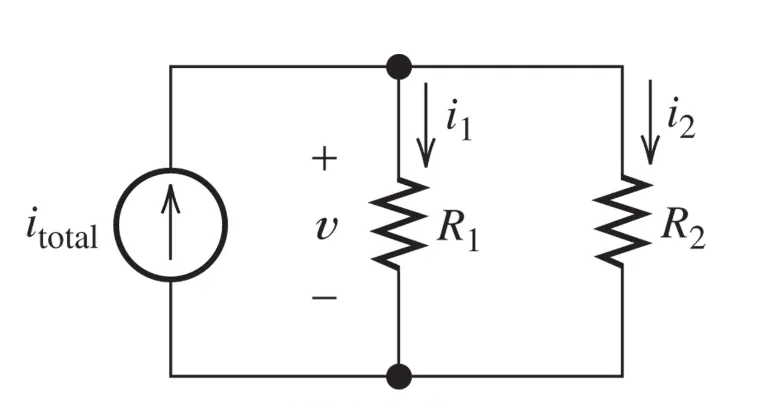 $$
R_{eq} = \frac{R_1\ R_2}{(R_1 + R_2)} \newline
V = i_{total}\ R_{eq} \newline
$$
$$
R_{eq} = \frac{R_1\ R_2}{(R_1 + R_2)} \newline
V = i_{total}\ R_{eq} \newline
$$
We can find equations for the relative currents: $$ I_1 = \frac{V}{R_1} = I_{total}\ \frac{R_2}{(R_1 + R_2)} \newline I_2 = \frac{V}{R_2} = I_{total}\ \frac{R_1}{(R_1 + R_2)} \newline $$