In this part we’ll cover electromagnetic waves - we’ll see why electrical and magnetic fields always appear together.
Displacement current
If we recall Faraday’s law: $$ \oint \mathbf{\vec{E}} \cdot d\mathbf{\vec{s}} = -\dfrac{d \Phi_B}{dt} $$
This says that a change in the magnetic field will produce an electrical field. But how about the converse?
Does a change in an electrical field produce a magnetic field?
If we consider this example with a capacitor being charged:
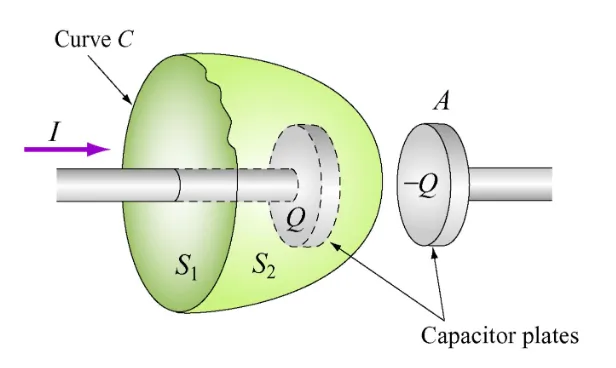
Using Ampere’s law: $$ \oint \mathbf{\vec{B}} \cdot\ d\mathbf{\vec{s}} = \mu_0 I_{enc} $$
If we look at $S_1$, we see that $I_{enc} = I$ - however, for $S_2$, $I_{enc} = 0$ - but the current does continue?
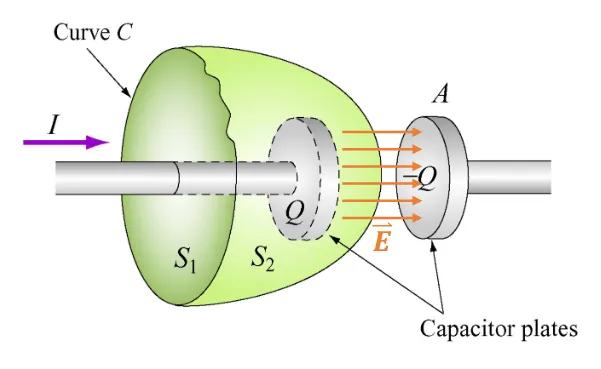
So we will need to add an extra term to Ampere’s law: $$ \oint \mathbf{\vec{B}} \cdot\ d\mathbf{\vec{s}} = \mu_0(I + I_d) $$
Where the displacement current, $I_d$: $$ I_d = \varepsilon_0 \dfrac{d \Phi_E}{dt} $$
In practice, $I = I_d$, thus the choice of the Amperian loop is inconsequential!
Gauss’s Law
For electrostatics, Gauss’s law said that: $$ \Phi_E = \oiint \mathbf{\vec{E}} \cdot\ d\mathbf{\vec{A}} = \dfrac{q}{\mu_0} $$
But in the case for magnetism - magnetic monopoles do not exist (meaning that $q = 0$). Therefore: $$ \Phi_B = \oiint \mathbf{\vec{B}} \cdot\ d\mathbf{\vec{A}} = 0 $$
Maxwell’s Equations
With these new tools in mind - we have now learned the four Maxwell equations that form the basis of electromagnetism!
Let’s write them all down:
Gauss’s Law for electrostatics: $$ \Phi_E = \oiint \mathbf{\vec{E}} \cdot\ d\mathbf{\vec{A}} = \dfrac{q}{\mu_0} $$
Gauss’s Law for magnetism: $$ \Phi_B = \oiint \mathbf{\vec{B}} \cdot\ d\mathbf{\vec{A}} = 0 $$
Faraday’s Law: $$ \varepsilon = \oint \mathbf{\vec{E}} \cdot d\mathbf{\vec{s}} = -\dfrac{d \Phi_B}{dt} $$
Ampere-Maxwell Law: $$ \varepsilon = \oint \mathbf{\vec{B}} \cdot d\mathbf{\vec{s}} = \mu_0(I + I_d) = \mu_0\left(I + \varepsilon_0 \dfrac{d \Phi_E}{dt}\right) $$
If the absence of sources is present (meaning that q = 0 and I = 0) - all of these become quite compact and tidy:
Gauss’s Law for electrostatics: $$ \Phi_E = \oiint \mathbf{\vec{E}} \cdot\ d\mathbf{\vec{A}} = 0 $$
Gauss’s Law for magnetism: $$ \Phi_B = \oiint \mathbf{\vec{B}} \cdot\ d\mathbf{\vec{A}} = 0 $$
Faraday’s Law: $$ \varepsilon = \oint \mathbf{\vec{E}} \cdot d\mathbf{\vec{s}} = -\dfrac{d \Phi_B}{dt} $$
Ampere-Maxwell Law: $$ \varepsilon = \oint \mathbf{\vec{B}} \cdot d\mathbf{\vec{s}} = \mu_0(I + I_d) = \mu_0 \varepsilon_0 \dfrac{d \Phi_E}{dt} $$
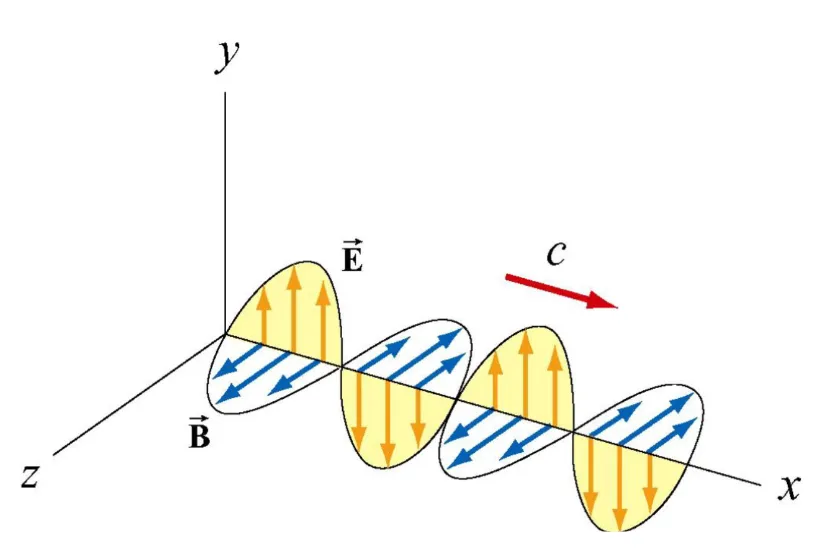
Now we can see, from Faraday’s law and Ampere-Maxwell’s Law that, if we have a change in one field - we’ll see a change in the other!
We’ll see why this picture will make a lot of sense soon:
Inductance
We have seen some aspect of inductances already - the induced current.
Imagine this scenario:
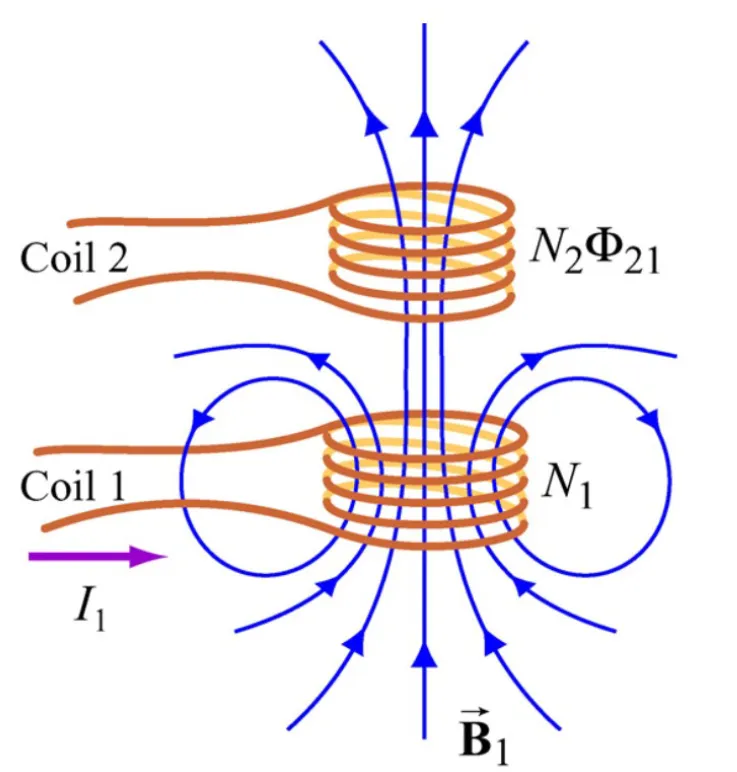
We can see that our $\mathbf{\vec{B_1}}$ passes through the second coil, therefore a flux is generated, $\Phi_{21}$
As we learned last time, varying $I_1$ will induce an emf!
Which means: $$ \varepsilon_{21} = -N_{2} \dfrac{d \Phi_{21}}{dt} $$
If we want to write this in terms of $I_1$ we get: $$ \varepsilon_{21} = M_{21} \dfrac{d I_1}{dt} $$
Where $M_{21}$: $$ M_{21} = \dfrac{N_2 \Phi_{21}}{I_1} $$
But let’s say that we vary $I_2$, this will also lead to an EMF, but in the first coil: $$ \varepsilon_{12} = -N_{1} \dfrac{d \Phi_{12}}{dt} = M_{12} \dfrac{d I_2}{dt} $$
Then, if we use the theorem of reciprocity - which states that:
The current at one point in a circuit due to a voltage at a second point is the same as the current at the second point due to the same voltage at the first.
Using this and combining Ampere’s law and the Biot-Savart law - we get: $$ M_{12} = M_{21} = M $$
This means - sending varying current (AC) through coil 1 - will generate an AC current in coil 2 as well!
We can also connect this to voltage, potential drop: $$ \dfrac{V_2}{V_1} = \dfrac{N_2}{N_1} $$
Self-Inductance
Say we only have one coil
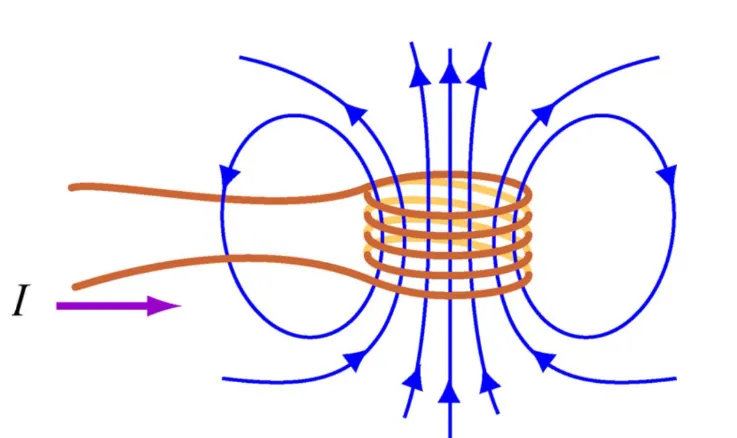
If we vary, $I$, an induced EMF will oppose the change in flux, according to Faraday’s law.
We denote this self-inducted EMF with, $\varepsilon_L$.
We can write it as: $$ \varepsilon_L = -N \dfrac{d \Phi_B}{dt} $$
We can relate this self-inductance with self-inductance, $L$: $$ \varepsilon_L = -L \dfrac{dI}{dt} $$
We can also write: $$ L = \dfrac{N \Phi_B}{I} = \dfrac{\mu_0 N^2 A}{l} $$
Therefore, the inductance, is a measure of an inductor’s resistance to change of the current!
In even simpler terms - inductors oppose change in the current!
So, since inductors oppose changes to the current - work must be done to establish a current in the inductor. Thus, energy must be stored in the magnetic field in an inductor! Similar to electrical fields in a capacitor.
The power, or the rate at an external EMF, $\varepsilon_{ext}$, works to overcome the self-induced EMF, $\varepsilon_L$, to pass the current $I$: $$ P_L = \dfrac{d W_{ext}}{dt} = I \varepsilon_{ext} = -I \varepsilon_L = IL \dfrac{dI}{dt} $$
This assumes that only $\varepsilon_{ext}$ and the inductor is present.
The total work done by an external source to increase the current from 0 to $I$ is: $$ W_{ext} = \int dW_{ext} = \int_0^I IL\ dI = \boxed{\dfrac{1}{2}LI^2} $$
Electromagnetic waves
We’ll now cover a very cool phenomena - we’ll cover why electromagnetic waves travel at light speed!
To prove this we’ll need to rewrite our definition for $\mathbf{\vec{E}}$ and $\mathbf{\vec{B}}$: $$ \mathbf{\vec{E}} = E_y(x, t)\mathbf{\vec{J}} = E\ cos(kx - \omega t)\mathbf{\vec{J}} $$
$$ \mathbf{\vec{B}} = B_z(x, t)\mathbf{\vec{K}} = B\ cos(kx - \omega t)\mathbf{\vec{K}} $$
Using Faraday’s law: $$ \oint \mathbf{\vec{E}} \cdot\ d\mathbf{\vec{s}} = - \dfrac{d}{dt} \iint \mathbf{\vec{B}} \cdot\ d\mathbf{\vec{A}} $$
If we take our ring integral inside a arbitrary rectangle - on the xy-plane:
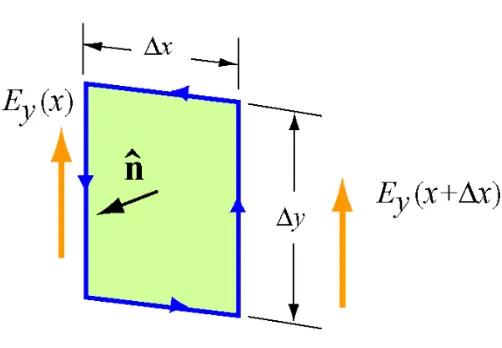
$$ E_y(x + \Delta x) - E_y(x) = - \dfrac{d}{dt} \iint \mathbf{\vec{B}} \cdot dxdy $$
We get that: $$ \dfrac{\partial E_y}{\partial x} = - \dfrac{\partial B_z}{\partial t} $$
Let’s calculate both: $$ \dfrac{\partial E_y}{\partial x} = -kE\ sin(kx - \omega t) $$
$$ \dfrac{\partial B_z}{\partial t} = \omega B\ sin(kx - \omega t) $$
Which, finally, means: $$ \boxed{\dfrac{E}{B} = \dfrac{\omega}{k} = c} $$
EMFs in circuits
Now that we have learned this beauty of electromagnetic waves - let’s tie it back to our electrical circuits.
As we learned with electrical fields and capacitor:
Electrical field opposes change in voltage $$ C = \varepsilon_0 \dfrac{A}{d} \newline U = \dfrac{1}{2} C|V^2| \newline I(t) = C \dfrac{dV}{dt} $$
We have now seen that, magnetic fields and inductors:
Magnetic field opposes change in the current $$ L = \mu_0 N^2 \dfrac{A}{l} \newline U = \dfrac{1}{2} LI^2 \newline V(t) = L \dfrac{dI}{dt} $$
We can now use this knowledge to understand LC and RLC circuits - and see how and why the energy oscillates between the electrical and magnetic field!