Dynamic systems
$u(t)$ - Input signal
$y(t)$ - Output signal
We usually represent our systems with ODEs of the form: $$ \dot{y} + ay = bu $$
Feedback systems
Using (positive or negative) feedback, meaning our input depends on the output as well!
$r(t)$ - Reference value/Setpoint
$e(t)$ = $r(t) - y(t)$ - Control error
Laplace Domain
$F(s)$ - Controller
$G_{uy}(s)$ = $\dfrac{Y(s)}{U(s)}$ - Transfer function
$L(s) = G_{uy}(s) F(s)$ - Loop transfer function
$G_{ry}(s)$ = $\dfrac{Y(s)}{R(s)} = \dfrac{L(s)}{1 + L(s)}$ - Closed-loop transfer function
Poles & Zeroes
Poles are given by $1 + L(s) = 0$ - the denominator in $G_{ry}(s)$ to determine the stability of a system.
Zeroes are given by $L(s) = 0$ - the numerator in $G_{ry}(s)$ to determine the system’s response
Controllers
P-controller
$$ u(t) = K_p \cdot e(t) $$
$$ U(s) = K_p \cdot E(s) $$
PI-controller
$$ u(t) = K_p \cdot e(t) + K_i \int_0^t e(\tau)\ d\tau $$
$$ U(s) = K_p \cdot E(s) + \frac{K_i}{s} \cdot E(s) $$
PD-controller
$$ u(t) = K_p \cdot e(t) + K_d \cdot \dfrac{d(e(t))}{dt} $$
$$ U(s) = K_p \cdot E(s) + sK_d \cdot E(s) $$
PID-controller
$$ u(t) = K_p \cdot e(t) + K_i \int_0^t e(\tau)\ d\tau + K_d \cdot \dfrac{d(e(t))}{dt} $$
$$ U(s) = K_p \cdot E(s) + \frac{K_i}{s} \cdot E(s) + sK_d \cdot E(s) $$
Feedback systems with noise/disturbance
Remaining control error, $e(\infty)$ when: $$ r(t) = r_0 \cdot \sigma(t) $$
$$ R(s) = \dfrac{r_0}{s} \ | \ \text{set } v(t) = 0 $$
$$ \begin{align*} \lim_{t \to \infty} e(t) & = \lim_{s \to 0} s \cdot E(s) \newline & = \lim_{s \to 0} s \cdot \left(R(s) - \dfrac{L(s)}{1 + L(s)} R(s)\right) \newline & = \lim_{s \to 0} s \cdot \left(R(s) \cdot \left(1 - \dfrac{L(s)}{1 + L(s)}\right)\right) \newline & = \lim_{s \to 0} s \cdot \left(R(s) \cdot \left(\dfrac{1 + L(s) - L(s)}{1 + L(s)}\right)\right) \newline & = \lim_{s \to 0} s \cdot \left(R(s) \cdot \left(\dfrac{1}{1 + L(s)}\right)\right) \newline & = \lim_{s \to 0} s \cdot \left(\dfrac{r_0}{s} \cdot \dfrac{1}{1 + L(s)}\right) \newline & = \lim_{s \to 0} \left(\dfrac{r_0}{1 + L(0)}\right) \newline & = \boxed{\lim_{s \to 0} \left(\dfrac{r_0}{1 + F(0)G(0)}\right)} \end{align*} $$
Remaining control error, $e(\infty)$ when: $$ v(t) = v_0 \cdot \sigma(t) $$
$$ V(s) = \dfrac{v_0}{s} \ | \ \text{set } r(t) = 0 $$
$$ E(s) = R(s) - Y(s) \newline $$
$$ E(s) = -Y(s) \newline $$
$$ E(s) = -\left(G(s) \cdot \left(V(s) + F(s) E(s)\right)\right) \newline $$
$$ E(s) = -G(s) V(s) - L(s) E(s) \newline $$
$$ E(s) + L(s) E(s) = -G(s) V(s) \newline $$
$$ E(s) \left(1 + L(s)\right) = -G(s) V(s) \newline $$
$$ E(s) = -\dfrac{G(s) V(s)}{1 + L(s)} \newline $$
$$ E(s) = -\dfrac{G(s)}{1 + L(s)} \cdot V(s) \newline $$
$$ \begin{align*} \lim_{t \to \infty} e(t) & = \lim_{s \to 0} s \cdot E(s) \newline & = \lim_{s \to 0} s \cdot -\dfrac{G(s)}{1 + L(s)} \cdot V(s) \newline & = \lim_{s \to 0} s \cdot -\dfrac{G(s)}{1 + L(s)} \cdot \dfrac{v_0}{s} \newline & = \lim_{s \to 0} -\dfrac{G(s) \cdot v_0}{1 + L(s)} \newline & = \boxed{\lim_{s \to 0} -\dfrac{G(0) \cdot v_0}{1 + L(0)}} \end{align*} $$
To eliminate the remaining control error all together, meaning that $e(\infty) = 0$ it means that $F(0) = \infty$. In others words, we need a $\frac{1}{s}$ component (an integral in the time domain) in our controller.
Physical models
Physical models are often model with ODEs, for example: $$ m\ddot{y}(t) = F(t) - ky(t) - b\dot{y}(t) $$
$$ m\ddot{y}(t) + b\dot{y}(t) + ky(t) = F(t) $$
Taking the Laplace transform $$ ms^2 Y(s) + bs Y(s) + kY(s) \stackrel{\mathcal{L}}{=} F(s) $$
$$ Y(s) \left(ms^2 + bs + k\right) = F(s) $$
$$ \boxed{G(s) = \dfrac{F(s)}{\left(ms^2 + bs + k\right)}} $$
We can also do this with state-space representation.
Rewriting our original ODE: $$ \ddot{y}(t) = -\frac{b}{m} \dot{y}(t) - \frac{k}{m} y(t) + \frac{1}{m} F(t) $$
Let $x_1 = y$ and $x_2 = \dot{y}$.
This means that: $$ \begin{cases} \dot{x_1} & = x_2 \newline \dot{x_2} & = -\dfrac{b}{m} x_2 - \dfrac{k}{m} x_1 + \dfrac{1}{m} F \end{cases} $$
Using Matrix notation: $$ x = \begin{bmatrix} \dot{x_1} \newline \dot{x_2} \end{bmatrix} = \begin{bmatrix} 0 & 1 \newline -\frac{k}{m} & -\frac{b}{m} \end{bmatrix} \begin{bmatrix} x_1 \newline x_2 \end{bmatrix} + \begin{bmatrix} 0 \newline \frac{1}{m} \end{bmatrix} F $$
$$ y = \begin{bmatrix} 1 & 0 \end{bmatrix} \begin{bmatrix} x_1 \newline x_2 \end{bmatrix} + \begin{bmatrix} 0 \end{bmatrix} F $$
Generalization
$$ \dot{x} = Ax + Bu \newline y = Cx + Du $$
$$ G_{uy}(s) = \dfrac{Y(s)}{U(s)} = C(sI - A)^{-1} B + D $$
Characteristics equation
To find the poles of the system in matrix notation we use the fact that the denominator of the transfer function is: $$ det(sI - A) $$
So, to find the poles we simply: $$ det(sI - A) = 0 $$
Reminder that: $$ A = \begin{bmatrix} a & b \newline c & d \end{bmatrix} $$
$$ det(A) = \dfrac{1}{ad - bc} $$
$$ A^{-1} = \dfrac{1}{ad - bc} \begin{bmatrix} d & -b \newline -c & a \end{bmatrix} $$
NB: This rule only applies for 2x2 matrices.
State feedback
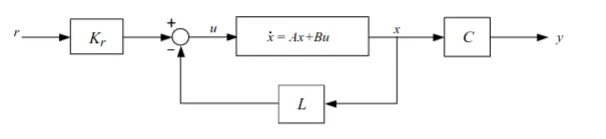 $$
u = K_r \cdot r - Lx \newline
y = Cx
$$
$$
u = K_r \cdot r - Lx \newline
y = Cx
$$
$$ \dot{x} = Ax + Bu = Ax + B(K_r r - Lx) \newline sX(s) = AX(s) + B(K_r R(s) - LX(s)) \newline sX(s) = AX(s) + BK_r R(s) - BLX(s) \newline sX(s) - AX(s) + BLX(s) = BK_r R(s) \newline X(s) (sI - A + BL) = BK_r R(s) \newline X(s) = (sI - A + BL)^{-1} BK_r R(s) \newline $$
$$ Y(s) = CX(s) \newline Y(s) = C (sI - A + BL)^{-1} B K_r R(s) \newline G_{ry}{s} = \dfrac{Y(s)}{R(s)} = C (sI - A + BL)^{-1} B K_r $$
We can determine K_r for a system with the knowledge that $G(0) = 1$
So: $$ K_r = \dfrac{1}{C(-A + BL)^{-1}) B} $$
Poles are given by: $$ det(sI - A + BL) = 0 $$
Stability
A system is stable if and only if its characteristic equation has roots in the LHP, meaning that $\Re(s) < 0$.
For systems of order 2, this means that all the coefficients are $> 0$
For systems or order 3 or higher we use Routh–Hurwitz method.
Nyquists simplified criterion
To use the Nyquists simplified criterion, $L(s)$ can not have a pole in the RHP. If this criterion is met, plot $L(j\omega)$ for $0 \leq \omega \leq \infty$.
If $L(j\omega)$ passes through the negative real axis with $(-1, 0)$ to its left, then the system is stable.
Nyquists criterion
If $L(s)$ has a pole in the RHP, we can still use Nyquists criterion.
$$ Z = P + N = \text{Number of zeroes } 1 + L(s) \text{ has in RHP.} $$
$$ P = \text{Number of poles } L(s) \text{ has in RHP.} $$
$$ N = \text{Number of turns } L(j\omega) \text{ has around } (-1, 0) \text{ clockwise.} $$