Signals
A signal is a set of information or data. Any physical quantity that varies over time, space or any other variable or variables.
Even, Odd & Periodic
An even function is symmetrical about the vertical axis. Mathematically this means: $$ f(t) = f(-t) \newline f[k] = f[-k] $$
An odd function is anti-symmetrical about the vertical axis. Mathematically this means: $$ f(t) = -f(-t) \newline f[k] = -f[-k] $$
A periodic function has a fundamental period (minimum), $T_0$. Which also means it has a fundamental frequency, $f_0 = \dfrac{1}{T_0}$. $$ f(t) = f(t + nT_0) \newline f[k] = f[k + nK_0] $$
We sometimes define the fundamental frequency in angular velocity instead of Hz, which means, $\omega_0 = 2\pi f_0 = \dfrac{2\pi}{T_0}$.
Convolution
Let’s call our input signal $x(t)$, our system operation for $h(t)$ and our output for $y(t)$. Assume that all of these are continuous functions, the convolution operation is denoted with $*$. $$ y(t) = x(t) * h(t) $$
The convolution operation is defined as: $$ y(t) = x(t) * h(t) = \int_{-\infty}^{+\infty} x(\tau)h(t - \tau) d\tau $$
In the discrete case: $$ c[k] = f[k] * g[k] = \sum_{m = -\infty}^{+\infty} f[m]g[k - m] $$
This operation is also:
Commutative: $$ f_1(t) * f_2(t) = f_2(t) * f_1(t) $$
Distributive: $$ f_1(t) * (f_2(t) + f_3(t)) = f_1(t)* f_2(t) + f_1(t) * f_3(t) $$
Associative: $$ f_1(t) * (f_2(t) * f_3(t)) = (f_1(t) * f_2(t)) * f_3(t) = $$
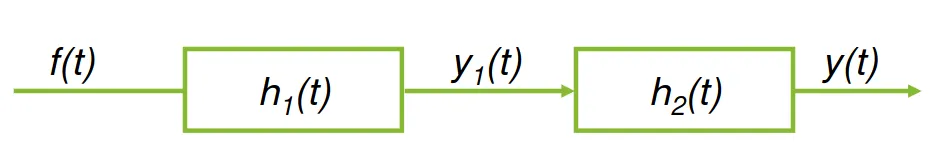
Using these properties we can say that:
$$ y(t) = f(t) * h(t) \ | \ h(t) = h_1(t) * h_2(t) $$
In the parallel case:
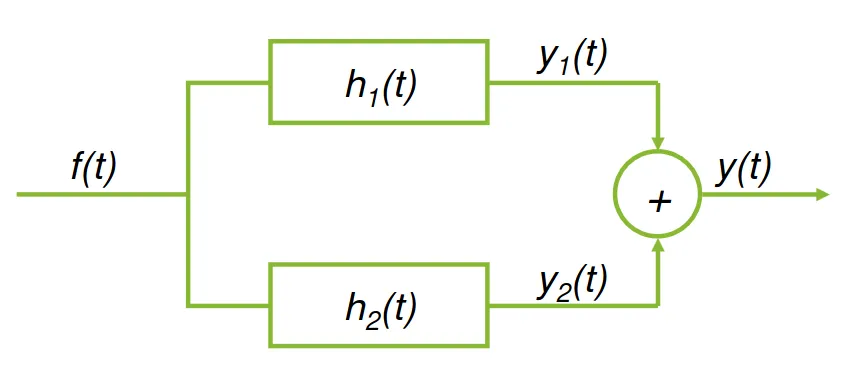
$$ f(t) * h(t) \ | \ h(t) = h_1(t) + h_2(t) $$
Shift: $$ f_1(t) * f_2(t) = c(t) \newline f_1(t) * f_2(t - T) = c(t - T) \newline f_1(t - T) * f_2(t) = c(t - T) \newline f_1(t - T_1) * f_2(t - T_2) = c(t - T_1 - T_2) \newline $$
Convolution with an impulse: $$ f(t) * \delta(t) = f(t) $$
We can combine these two: Convolution with an impulse: $$ f(t) * \delta(t - T) = f(t - T) $$
Differential Equations in the time-domain
As we defined, the output of these systems are the result of two independent cases.
So for the zero-input response: $$ Q(D)y_0(t) = 0 $$
The solution for $y_0(t)$ will be: $$ y_0(t) = c_1 e^{\lambda_1 t} + c_2 e^{\lambda_2 t} + \ldots + c_n e^{\lambda_n t} $$
If repeated roots: $$ y_0(t) = (c_1 + c_2t + \ldots + c_r t^{r - 1})e^{\lambda_1 t} + c_{r +1}e^{\lambda_{r + 1} t} + \ldots + c_n e^{\lambda_n t} $$
Also in the case we have complex roots, $\alpha \pm j \beta$. $$ y_0(t) = \dfrac{c}{2} e^{j \theta} e^{(\alpha + j \beta)t} + \dfrac{c}{2} e^{-j \theta} e^{(\alpha - j \beta)t} = \dfrac{c}{2} e^{\alpha t} \left[ e^{j(\beta t + \theta)} + e^{-j(\beta t + \theta)}\right] $$
Using Euler’s formula: $$ y_0(t) = c e^{\alpha t} cos(\beta t + \theta) $$
Example
$$ (D^2 + 3D + 2)y_0(t) = 0 $$
$$ \lambda^2 + 3\lambda + 2 = (\lambda + 1)(\lambda + 2) = 0 $$
$$ \lambda_1 = -1 \newline \lambda_2 = -2 $$
$$ y_0(t) = c_1 e^-t + c_2 e^{-2t} $$
Trigonometric Fourier series
$\omega_0$ is called the fundamental frequency
$n \omega_0$ is called the $n$th harmonic.
We can call the fundamental period for, $T_0$: $$ T_0 = \dfrac{2\pi}{\omega_0} $$
So: $$ f(t) = a_0 + a_1 cos \omega_0 t + a_2 cos 2\omega_0 t + b_1 sin \omega_0 t + b_2 sin 2\omega_0 t + \ldots $$
We can write this more compactly. $$ a_n cos n\omega_0 t + b_n sin n\omega_0 t = C_n cos(n\omega_0 t + \theta_n) $$
Where: $$ C_n = \sqrt{a_n^2 + b_n^2} $$
$$ \theta_n = tan^{-1} \left(\dfrac{-b_n}{a_n}\right) $$
So: $$ f(t) = C_0 + \sum_{n = 1}^{\infty} C_n cos(n\omega_0 t + \theta_n) $$
Exponential Fourier series
$$ f(t) = \sum_{-\infty}^{\infty} D_n e^{jn\omega_0 t} $$
$$ C_n cos(n\omega_0 t + \theta_n) = \dfrac{C_n}{2} \left(e^{j(n\omega_0 t + \theta_n)} + e^{-j(n\omega_0 t + \theta_n)}\right) $$
$$ \left(\dfrac{C_n}{2} e^{j\theta_n}\right) e^{jn\omega_0 t} + \left(\dfrac{C_n}{2} e^{-j\theta_n}\right) e^{-jn\omega_0 t} $$
$$ D_n = \dfrac{1}{2} C_n e^{j\theta_n} $$
$$ D_{-n} = \dfrac{1}{2} C_n e^{-j\theta_n} $$
$$ f(t) = D_0 + \sum_{n = 1}^{\infty} D_n e^{jn\omega_0 t} + D_{-n} e^{-jn\omega_0 t} $$
$$ f(t) = \sum_{-\infty}^{\infty} D_n e^{jn\omega_0 t} $$
Definition
$$ F(\omega) = \int_{-\infty}^{\infty} f(t) e^{-j\omega t}\ dt $$
$$ f(t) = \dfrac{1}{2\pi} \int_{-\infty}^{\infty} F(\omega) e^{j\omega t}\ d\omega $$
$$ f(t) \iff F(\omega) $$
Example
$$ f(t) = rect\left(\dfrac{t}{\tau}\right) $$
$$ F(\omega) = \int_{-\infty}^{\infty} rect\left(\dfrac{t}{\tau}\right) e^{-j\omega t}\ dt $$
$$ F(\omega) = \int_{-\frac{\tau}{2}}^{\frac{\tau}{2}} e^{-j\omega t}\ dt $$
$$ F(\omega) = -\dfrac{1}{j\omega} e^{-j\omega t} \bigg\rvert_{\frac{\tau}{2}}^{-\frac{\tau}{2}} $$
$$ F(\omega) = -\dfrac{1}{j\omega} \left(e^{-j\omega \dfrac{\tau}{2}} - e^{j\omega t \dfrac{\tau}{2}}\right) $$
$$ F(\omega) = \dfrac{2 sin\left(\dfrac{\omega \tau}{2}\right)}{\omega} $$
$$ F(\omega) = \tau \dfrac{sin\left(\dfrac{\omega \tau}{2}\right)}{\dfrac{\omega \tau}{2}} $$
$$ F(\omega) = \tau sinc\left(\dfrac{\omega \tau}{2}\right) $$
$$ rect\left(\dfrac{t}{\tau}\right) \iff \tau sinc\left(\dfrac{\omega \tau}{2}\right) $$
Transfer function
Say we have a system which can be modeled as: $$ y(t) = f(t) * h(t) $$
The same system, but in the frequency domain is therefore: $$ Y(\omega) = F(\omega)\ H(\omega) $$
Just as we call, $h(t)$, the system response function, we call $H(\omega)$ for the spectral response of the system.
Since, in the most general case, we view our frequency functions as complex functions. We can say that
An input signals spectral component of frequency, $\omega$, is modified in amplitude by a factor of, $|H(\omega)|$ and shifted in phase by an angle of $\angle H(\omega)$
However, since we modify the phase, this means that our output signal may have a different waveform than our input.
Nyquist-Shannon sampling theorem
A real signal whose bandwidth is limited to $B$ Hz can be reconstructed exactly from its samples if the sampling frequency is $\mathcal{F}_s > 2B$.
Definition
The Laplace transformation is a unilateral transform, which just means it is one-sided.
Given a function that is defined for $t \geq 0$, and it is locally integrable, meaning that its integral exists in every finite interval of $[0, \infty)$
$$ F(s) = \int_0^{\infty} f(t)e^{-st}\ dt \newline F(s) = \mathcal{L}[f(t)] $$