Introduction
Vision is a very fundamental sense for humans. When looking at a scene, our eye(s) work as an image acquisition device. This “image” is then sent to our image interpretation system, the brain, for further processing, and then we finally yield a perception of the scene.
Similarly, in computer vision, we try to mimic this process. Cameras are used as image acquisition devices, and computers are the image interpretation system.
Image Data
Firstly, before we even can represent an image digitally, we need to form it.
A few components of the image formation process are,
- Perspective projection.
- Light scattering (when hitting a surface).
- Lens optics.
- Color filtering (e.g., Bayer color filter array 1).
Secondly, the color space of a picture is (usually) represented in Red, Green, and Blue (RGB) channels.
These can be (numerically) represented both as integers — e.g., uint8 which yields the range $[0, 255]$ — or as floating-point numbers — e.g., float32 which yields the range $[0, 1]$.
RGB is a linear color space (i.e., the color space is a linear combination of the three channels) and has single wavelength primaries (i.e., the three channels correspond to three different wavelengths of light).
There are other color spaces, such as Hue, Saturation, Value (HSV), which are more intuitive for humans to understand 2.
Remote Sensing Data
Remote sensing is the science of acquiring information about an object without being in physical contact with it.
For example, satellite imagery is a form of remote sensing. Satellite imagery has different spatial resolutions, (can have) various spectral bands, and different acquisition times (temporal resolution).
We will also do some preprocessing of the images. This can include, corrections for lens distortion (e.g., radial distortion), histogram equalization (to enhance contrast), and radio- or geometric corrections (to align images to be true orthophotos 3).
There are more details, but this really is not my area of interest (sorry Mohammad if you are reading this :]).
Let’s talk about more interesting stuff. Neural Networks.
Neural Networks
Let’s start with a single neuron.
Recall logistic regression. The logistic function (or sigmoid function) is defined as,
$$ f(x) = \frac{1}{1 + e^{-x}}, $$
here $f : \mathbb{R} \to [0, 1]$, so we can take in a continuous input and output a probability (quite powerful).
Thus, we can have as input,
$$ X = w_1 x_1 + w_2 x_2 + \ldots + w_m x_m + b. $$
And then we can apply the logistic function to $X$ to get the output.
We call the $x_1, x_2, \ldots, x_m$ the input features, and the $w_1, w_2, \ldots, w_m$ the corresponding weights.
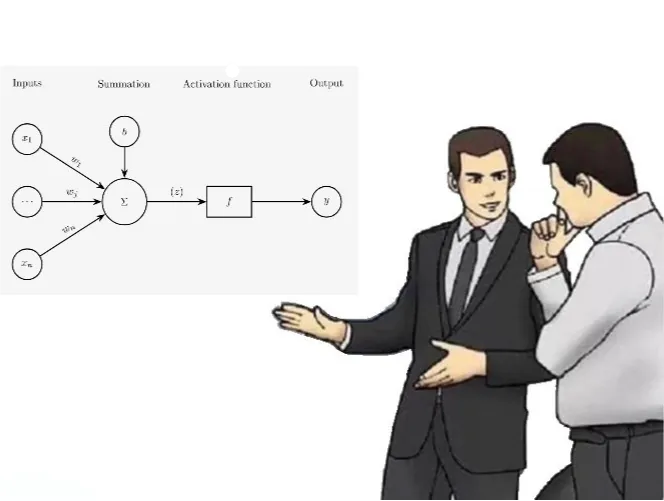
Now, let’s stack em (if you want prettier figures, go to this.
Now, for the part I’ve been wanting to write about, classical computer vision.
Classical Computer Vision
A very important topic in (classical) computer vision is neighborhood information and neighborhood processes.
For example, linear filtering can be defined as,
$$ G[i, j] = \frac{1}{(2k + 1)^2} \sum_{u = -k}^{k} \sum_{v = -k}^{k} F[i + u, j + v], $$
where $F$ is the input image, $G$ is the output image, and $k$ is the kernel size.
Smoothing can be defined as,
$$ \begin{align*} G[i, j] &= \sum_{u = -k}^{k} \sum_{v = -k}^{k} H[u, v] F[i + u, j + v] \newline G &= H \ast F, \end{align*} $$
where $H$ is the kernel.
Another very important type of process is derivatives,
$$ \begin{align*} \frac{\partial f}{\partial x} & = \lim_{\varepsilon \to 0} \frac{f(x + \varepsilon, y) - f(x, y)}{\varepsilon} \newline & = \frac{\partial h}{\partial x} \approx h_{i+1, j} - h_{i, j} \newline & = \mathcal{H} = \begin{bmatrix} 0 & 0 & 0 \newline 1 & 0 & -1 \newline 0 & 0 & 0 \end{bmatrix}, \end{align*} $$
where the last step is an example matrix (kernel) for the derivative.
With these matrices and performing partial derivatives in both $x$ and $y$ directions, we can have an edge detector.